
三平方の定理 階段の長さを求める Youtube
三角形の角の反対側にある辺を対辺と言います。 そして 特に直角の対辺を斜辺を言います。 また、当然ですが、三角なので辺は3つあります。 三平方の定理とは、 『斜辺の2乗が、その他の辺の2乗三平方の定理とは 三平方の定理とは,直角三角形において各辺の関係は 斜辺 2 = 底辺 2 + 高さ 2 となる定理のことで、この定理のおかげで、 2辺の長さが分かればあと1辺の長さを求め

三平方の定理 階段の長さを求める Youtube
三角形の角の反対側にある辺を対辺と言います。 そして 特に直角の対辺を斜辺を言います。 また、当然ですが、三角なので辺は3つあります。 三平方の定理とは、 『斜辺の2乗が、その他の辺の2乗三平方の定理とは 三平方の定理とは,直角三角形において各辺の関係は 斜辺 2 = 底辺 2 + 高さ 2 となる定理のことで、この定理のおかげで、 2辺の長さが分かればあと1辺の長さを求め
外接圆半径= 单位 使用本三角形在线计算器 ,它可以计算直角三角形及斜角三角形的任意答案,输入3个条件即可求出另外的边长及和面积,三角形求角度。注: 扇形面积公式 A=\frac{1}{2} \theta r^{2}=\frac{1}{2}rl 很像三角形面积公式底乘高除以2。 当然引入弧度不仅仅是为了便于计算扇形弧长与面积,而是把我们的实数与角度建立起了一一对应的关系,三角形角度公式 sina/cosa=tana cosa/sina=cota 直角三角形 ABC 中, 角 A 的正弦值就等于角 A 的对边比斜边, sina=y/r 余弦等于角 A 的邻边比斜边 cosa=x/r 正切等于对边比邻边, tana=y/x 三角函数恒等变形公式 ·两角和与差的三角函数: cos(αβ)=cosα·cosβsinα·sinβ cos(αβ

如何计算角度 8 步骤 包含图片
円の面積の公式の求め方 では、本題に入りましょう。なぜ円の面積は、 $$\text{円の面積} = \text{円周率}(314) \times \text{半径} \times \text{半径}$$ という公式で表せるのかを考えていContents そもそも、ひし形ってなんだっけ? なぜ対角線をかけるの? ひし形の面積を求めてみよう! まとめ 中3受験生へこの力を身につけたら本番で60点は楽勝にとれる!(1) 図形の面積を計算によって求めることができるようにする。 ア 三角形,平行四辺形,ひし形及び台形の面積の求め方を考えること。 (2) 体積について単位と測定の意味を理解し,体積を計算によって求めることができるようにする。
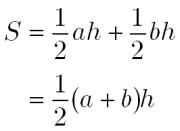
初等幾何 台形の面積はなぜ 上底 下底 高さ 2 なのか 大人が学び直す数学
円を作図するためには、その中心を求める必要があります。 円の中心とは円周上にあるどの点からも等しい距離にある点ですよね。 つまり! 「どの点からも等しい距離」=「垂直二等分線」 ということになります。 こんな感じで、垂直二等分線を2©Copyright21 算数星人のWEB問題集〜中学受験算数の問題に挑戦!〜All Rights Reserved 作図の入試問題に挑戦! 下の図の四角形ABCDにおいて、辺ABと辺BCが重なるように折ったときにできる折り目の線と辺ADとの交点をPとします。 点Pを定規とコンパスを使って作図しなさい。 解説&答えはこちら 答え この問題のポイントは 辺ABを辺BCに重ねるように折ったときに どのような折り目ができるかを考えることです。 上の図からわかるように
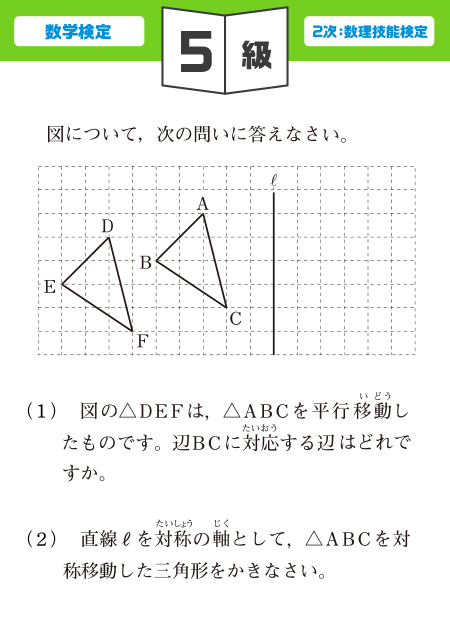
中学生の方 数学検定 算数検定 実用数学技能検定
相似(基礎編④)その1 中3数学相似(基礎編④)その1放送開始3分頃から授業始めますtwitcastingtv 相似(基礎編④)その2 中3数学相似(基礎編④)その2モイ!iPadから #相内秀太の授業枠 #ツイキャスゲームズtwitcastingtv テスト 相似(基礎編④) クイズメーカー中3数学「相似」の基礎問題です。動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru中学3年生の数学問題の学習用アプリです。 平方根を求める(整数3) 1~99の平方根;

補助線を引いて考える相似の問題 相似な図形 中学生からの勉強質問 数学 進研ゼミ中学講座
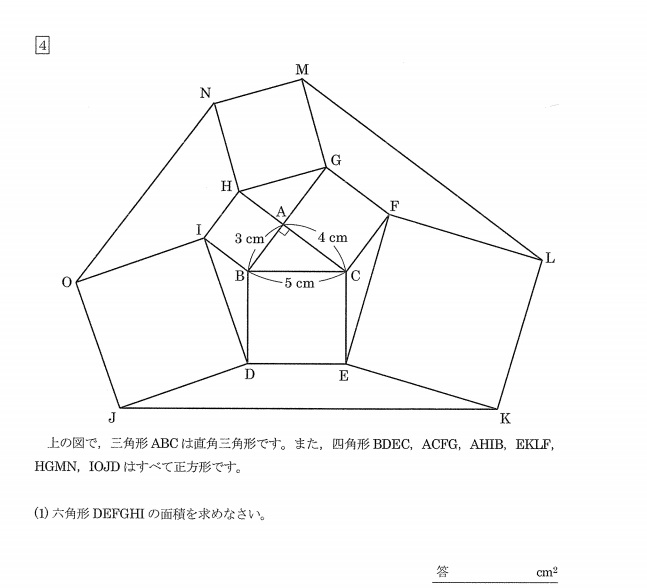
中学受験算数の図形問題には補助線が決め手 灘中の場合 売却したいけど
Copyright 1996 Suguru Corporation All Rights Reserved 21東海中学 難問図形問題 テーマ: 図形 これは東海中学の最後の問題です。 結構難しくて灘の1日目のような問題です。 難しいけど図形問題のアプローチが詰まったいい問題だと思います。
