画像 扇形面積 公式 弧度法 114738-扇形面積 公式 弧度法

扇形の面積 面積も弧の長さと同様に比例式を使います。 扇形の面積も中心角の大きさに比例するので，半径\(r\)の円の面積は\(\pi r^{2}\)，中心角\(2\pi\)なのでさがtrad である扇形で囲まれる図形の面積は 1 2 r2t である． 例 半径が5 であり中心角の大きさが3rad である扇形で囲まれる図形の面積は 1 2 ×52×3= 75 2 終 問題1015 半径が3 であり中心角の大きさが 8π 7 rad である扇形で囲まれる図形 の面積を求めなさい．扇形,I,醐半臥 単軌 円周率×ミ宗 を学ぶが,これが 弧の長さ = 半径×中心角の弧度 扇形の面稚 = 半径×半径×中心角の弧度T2 = 半径×弧の長さT2 となる特に扇形の面紗よ三角形の面積とr同じ｣ と見なせることがわかる 二のこと1つをとっても弧度の図形的な扱い

弧度制 弧度与角度的互化的知识点总结 相关视频及试题在线练习 易学啦

扇形面積 公式 弧度法

扇形面積 公式 弧度法-扇形の弧の長さと面積を，弧度法をもちいて表してみよう． 図のように半径が r ,中心角が θ の扇形の弧の長さを l ,面積を S とすると，弧度法の定義より θ = l r だから ∴ l = r θ (1) 面積と中心角の比から S θ = π r 2 2 π ∴ S = 1 2 r 2 θ (2) 以上， (1) ， (2) より， S = 1 2 r l となる．さて、弧度法を使うことにより何が変わるかというと、例えば、扇形の弧の長さや 面積を求める式が以下のように変わります。 半径 r 、中心角d°＝θ rad の扇形について、

扇形的弧長與面積

 扇形の面積の公式弧度法 半径が r 、中心角が \theta (\mathrm {rad}) の扇形の面積 S は \begin {align} \color {red} {S = r^2 \pi \cdot \frac {\theta} {2\pi} = \frac {1} {2} r^2 \theta} \end {align} 弧度法では 360^\circ が 2\pi \ \mathrm {rad} に対応するので、中心角の割合は「 \displaystyle \frac {\theta} {2\pi} 」となります。 扇形面積公式 公式 推導過程 注意事項 中文百科全書版之國小數學複合圖形面積之數位教材 ö 3 國小六年級數學複合圖形面積教學教材主要 é為 ( 與扇形面積運 算 ) õ ( 與三角形複合圖形面積運算 ) õ ( 與矩形複合圖形面積運 算 ) õ ( 與梯形複合圖形面積運算 ) õ ( õ三角形 õ矩形複合圖形面

 中心角がθである扇形の弧の長さl、面積Sを求めるための公式は以下の通りです。 半径rの円の円周の長さは2πr、面積は\(πr^2\)であるのは既に習いましたよね。 扇形の弧の長さや、面積は中心角に比例します。 そのため扇形の円周の長さや面積は扇形の面積扇形ocbは比例関係 2π h =π 扇形OCB （ラディアンを使った場合） 360 h =π 扇形OCB （度を使った場合）性質。除扇形面積公式。 sIV15 認識線與線、線與平面在空間中的垂直 關係和平行關係。不調整 sIV16 理解簡單的立體圖形及其三視圖與平面 展開圖，並能計算立體圖形的表面積、側面積及 6 理解平面圖形相似的意義，知道圖形 經縮放後其圖形相似，並能應

刪去 原 學習重點 42 「透過弧度法求弧長及 扇形面積」。 刪去在原學習重點 43 中的「理解其圖像。」 7 求導法 7 求導法 刪去 在 原 學習重點 73 的注釋 中 三條公式 ： (cot ) cosec もしおうぎ形ではなく円であれば、面積は πr2 π r 2 なので、比で考えると S πr2 = θ 2π S π r 2 = θ 2 π なので、これを S S について解くと S = 1 2r2θ S = 1 2 r 2 θ となります。 もちろんこれでもいいのですが、弧の長さの式を使ってさらに変形することもできます。 弧の長さを l l とすると、 l = rθ l = r θ なので、 S = 1 2rl S = 1 2 r l となります。 この式変形は単純です円周の長さ 2πr に対して、中心角の割合が θ/2π であるため もしくは、単純に、1ラジアンの円弧の長さ（＝半径（r））の θ倍であるため ・扇形の面積は （r 2 θ）/2 扇形の面積の公式：円弧×半径/2 に代入

A1 11 9 扇形 弓形面積 Youtube

扇形面积公式 扇形面积公式画法

 弧度法x radの中にπのニュアンスが含まれているので扇形の弧や長さの公式にπは現れません。 例題：次のものを求めよ。 (1) 半径3,中心角1radの扇形の弧の長さ (2) 半径5,中心角04radの扇形の面積 (3) 中心角05rad,弧の長さ4の扇形の面積弧度法で扇の弧の長さと面積を求める公式 弧度法を使って、扇の弧の長さと面積を求める公式を紹介します。 半径がr、中心角がθの扇の弧の長さをl、面積をSとするとき ※θは、度数法ではなく弧度法円弧の長さと扇形の面積 328 4．sinθ の値 9 5．cosθ の値 740 6．tanθ の値 1152 7．三角関数の相互関係① 804 8．三角関数の相互関係② 1545 9．y＝sin x のグラフ 1123 10．y＝cos x のグラフ 1155 11．y＝tan x のグラフ （準備中） 12．平行移動 （準備中）

扇形 簡介 組成部分 面積 弧長 周長 其他知識 中文百科全書

弧度制 扇形弧长公式 面积公式 数学作业 解题作业帮

4 續 三 角 函 數 4 續 三 角 函 刪去學習重點數 42「透過 弧度法求 長及扇形 面積 」。 刪去在學習重點43 中的「理解其圖 像 」。 7 求導法 7 求導法 刪去在學習重點 73 的注釋中三條公式： (cot x) cosec 2 x (sec x) sec tan (cosec x扇形の面積や周長を求めさせる際も，半円と 中心角の関係を基に具体例を示して活動させる。三角関数の性質の学習では，角度を表す図形と値 の正負を整理し，三角関数の相互関係や「sin（θ＋2nπ）＝sinθ」などの公式の理解へ つなげさせる。先ほど説明したように，半径1の扇形においては(中心角)=(弧の長さ)なので$\theta$でした． 左の扇形(半径1)と右の扇形(半径$r$)の相似比は$1r$ですから，弧の長さも当然$1r$となります． よって， 半径$r$の扇形の弧の長さは$r\theta$となりますね． 面積の公式

初中数学 求阴影部分面积 如何计算不规则扇形面积呢 哔哩哔哩 つロ干杯 Bilibili

扇形面积计算 万图壁纸网

 弧度法における面積公式 半径 r r r ，中心角 θ \theta θ ラジアンの扇型の面積は 1 2 r 2 θ \dfrac{1}{2}r^2\theta 2 1 r 2 θ 例えば，半径が 2 2 2 で中心角が π 4 \dfrac{\pi}{4} 4 π ラジアンである扇形の面積は， 1 2 × 2 2 × π 4 = π 2 \dfrac{1}{2}\times 2^2\times\dfrac{\pi}{4}=\dfrac{\pi}{2} 2 1 × 2 2 × 4 π = 2 π と計算できます。よって，扇形の面積の公式も導かれる。 4 Napierの数だって同じ ～発想は接線の傾きが1だったらいいなということ～ Napierの数は，x=0における接線の傾きが1になるというような指数関数y=a x から定義することができる。 一般角と弧度法、扇形の弧長l=rθと面積S=1/2r²θ スポンサーリンク 高校数学Ⅱ 三角関数 検索用コード 三角比から三角関数へ}} \\ 5zh 数Iでは,\ 三角比$\sin\theta,\ \cos\theta,\ \tan\theta$について学習した \\ 2zh 三角形の計量を目的としていたので

3

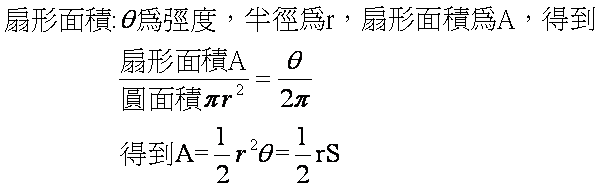
扇形的弧長與面積

すると， (91) の和が出来上がります。 したがって ∫∫Df(x, y)dxdy = ∫b a{∫d cf(x, y)dy}dx となること分かります。 ここで問題になるのは，領域 D が長方形であるとは限らないことです。 領域 D が長方形以外のとき，例えば，下のような図形になる場合 y のとり得る値の範囲は ψ(x) ≦ y ≦ ϕ(x) ですから (92) は次のようになります。 ∫∫Df(x, y)dxdy = ∫b a{∫ϕ ( x) ψ ( x) f扇形の弧の長さと面積の関係 扇形の弧の長さと面積を求める式を示します。 扇形の弧の長さ L=rθ 扇形の面積 S＝r^2θ/2＝rL/2 上式の通り、扇形の面積は、扇形の弧の長さLに半径rを掛けて2で除した値です。扇形の面積は下記が参考になります。扇形の面積 ← PC用は別頁→ 印刷用PDF版は別頁 == 扇形の面積 == 解説 円の面積Sを半径rを用いて表わすと， です。 （πは円周率：π=←無限に長い小数になるからギリシャ文字πで表すことになっている） 半円の面積は，円の面積の半分だから 3分の1円の面積は，円の面積の3分の1だか

Ppt 弧度制powerpoint Presentation Free Download Id

圓中有關計算 弧長 扇形面積和圓錐

 扇形の面積も弧度法で この流れで扇形の面積も求めてみましょう。やることは同じでまず度で考えます。 先程と同じように半径が \(r\) の扇形を考えて中心角を \(\alpha\) 度としましょう。扇の面積 続いて扇の面積について考えてみましょう。 円の面積はr×r×πで求められました。 先ほどと同じように考えます。 2πの角度のときにその面積はr×r×πです。 では角度がθのときはどうなるでしょうか。 2π：r×r×π＝θ：S これを整理すると ②（ただしθは弧度法で表したものに限る） また 弧度法で弧の長さと面積をだす公式が腑に落ちません弧の長さは、半径 x 中心角(ラジアン)面積は、半径 x この長さ x 1／2とのことですが、なぜ上記の公式で、弧の長さと、面積を求めることができるのでしょうか？π：円周率中心角

扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典

扇形平台钢格板怎么计算弧长和扇形面积 安平润潭金属网业www Runtanwangye Com

前回 https//googl/zBDZJZ 次回 https//googl/iSWs6k動画のプリント（19ch） http//www19chtv/サブチャンネル とある男が一、弧度與扇形周長與面積 (1)弧度制： (a)弧度量的定義： 設有一圓，圓心為O，半徑為r。在圓周上取一段圓弧 ∩ PQ ，使得圓弧 ∩ PQ 的 長度等於r，規定這一段圓弧 ∩ PQ 所對的圓心角∠POQ就定義成1 弧度。 (b)度與弧度之互換：扇形の面積を求める公式は、S = πr^2 × x/360 = 1/2 lr で表されます。このページでは、扇形の面積の求め方を、計算問題と共に説明しています。また、公式の導き方も説明しています。

圓的周長與面積 16 扇形弧長計算的練習 Youtube

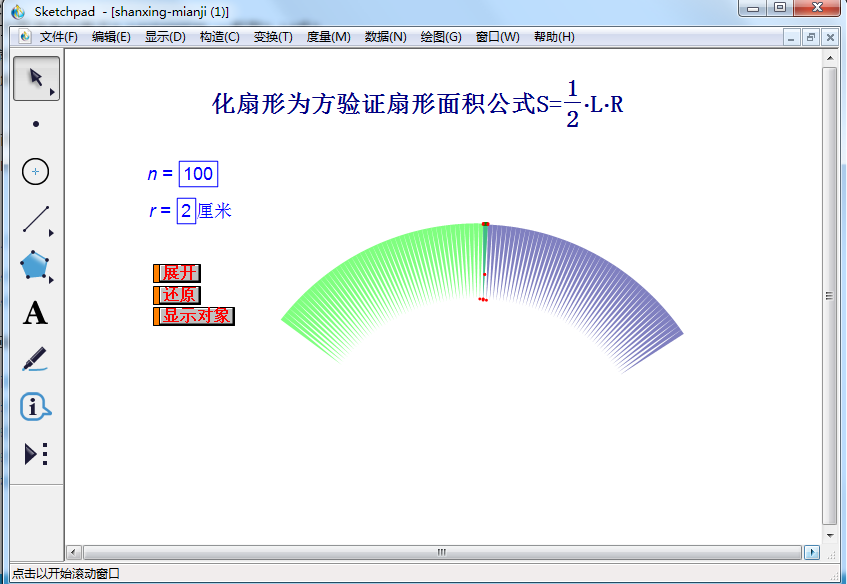
扇形面积公式是什么 如何推导 知乎

33 常態分布、信賴區間與信心水準的解讀 31不含系統抽樣、部落抽樣 二、三角函數 1一般三角函數的性質與圖形 11 弧度、弧長及扇形面積公式 12 倒數關係、商數關係、平方關係

半径不等的扇形面积 半径不等的扇形面积怎么算扇形 两条半径不相等 我没 三人行教育网 Www 3rxing Org

三角函数弧长和扇形面积公式 哔哩哔哩 つロ干杯 Bilibili

圆的周长与面积 弧长 扇形的面积 玄数

扇形面積公式推導 編程樂其中 數學不好 看你怎麼編 每日頭條

扇形面积的计算公式 扇形面积的计算公式画法

Q Tbn And9gctoaftep Cp0mxb1byahotggx3ub73wafwbkzah7fg7xmsh2anr Usqp Cau

扇形面积的计算公式 扇形面积的计算公式画法

09 11 27 01 圓與扇形 不學無數 隨意窩xuite日誌

扇形弧長與面積 106學年高職數學 B 第一冊 發現學習的美麗新世界

扇形面积计算 万图壁纸网

09 11 27 01 圓與扇形 不學無數 隨意窩xuite日誌

圓面積公式 圓面積公式是圓周率 半徑的平方 用字母可以表示為 S Pr 華人百科

中考數學圓中弧長及扇形的面積計算專題 1 每日頭條

半圆的面积公式怎么求 半圆的面积公式中文 半圆的面积怎么求

圓中有關計算 弧長 扇形面積和圓錐

2 3 弧度制一 素质教育目标 一 知识教学点1 弧度制的定义 2 用弧度制表示的弧长公式 扇形面积公式 Ppt Download

Q Tbn And9gcqgejm7nbeljjpoq4j3gwoy4cch2aapovxhwfsr Y2ji7bsp4dn Usqp Cau

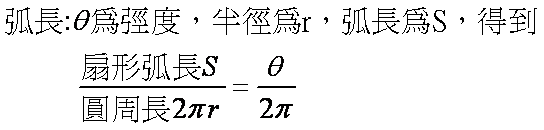
扇形的弧長與面積

弧长公式扇形面积公式 西瓜视频搜索

弧度制 弧度与角度的互化的知识点总结 相关视频及试题在线练习 易学啦

3 9 弧长及扇形的面积 哔哩哔哩 つロ干杯 Bilibili

扇形面积公式 扇形面积公式画法

Ppt 弧度制powerpoint Presentation Free Download Id

高中數學必修四 三角函數突破點 二 弧度制及其應用 每日頭條

圓的周長與面積 24 如何計算扇形的周長 Youtube

19 年高中数学1 1 2弧度制教学案新人教a版必修4下载 Word模板 爱问共享资料

扇形面积公式大全 搜狗图片搜索

扇形的弧長與面積

扇形面积公式大全 搜狗图片搜索

扇形面积公式计算公式 搜狗图片搜索

弧长及面积公式 腾讯视频

扇形面积公式 哔哩哔哩 つロ干杯 Bilibili

半圆的面积公式怎么求 半圆的面积公式中文 半圆的面积怎么求

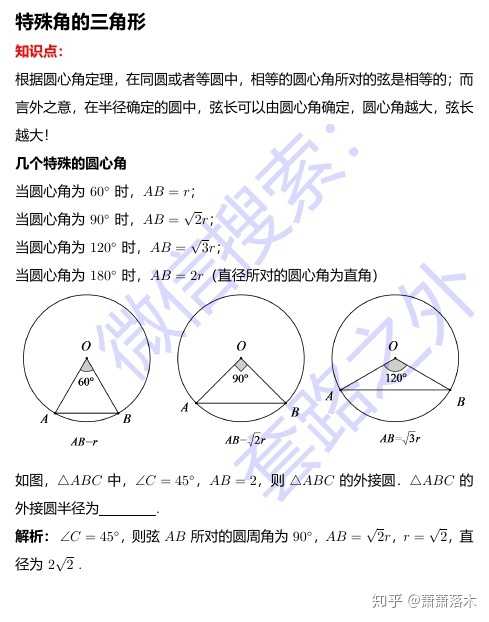
知道半径如何算圆心角 扇形的圆心角怎么求 圆锥展开图圆心角公式

利用弧度制证明扇形面积公式其中是扇形弧长 是圆的半径

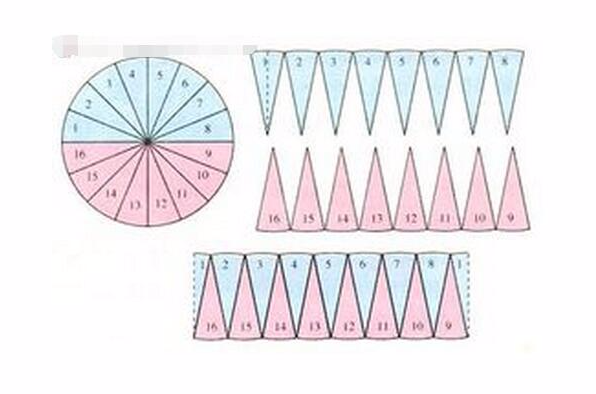
圓面積公式 圓形面積 來源故事 扇形 公式推導 圓面積公式 圓周長公式 中文百科全書

圓中有關計算 弧長 扇形面積和圓錐

三角函数03 扇形面积的计算 哔哩哔哩 つロ干杯 Bilibili

弧度计算公式 弧度计算公式 弧度 计算 公式

高中数学必修四 基础详细讲义附答案38页 小初高题库试卷课件教案网

圆面积公式 快懂百科

基礎 給扇形面積求圓心角 Youtube

扇形面积公式 腾讯视频

圓的周長與面積 27 扇形的複合圖行計算2 Youtube

扇形面积的计算公式 扇形面积的计算公式画法

24 4弧长和扇形面积 哔哩哔哩 Bilibili

圆面积公式 快懂百科

圓面積公式弧度單元四 Bedachun

扇形面积公式 扇形面积公式画法

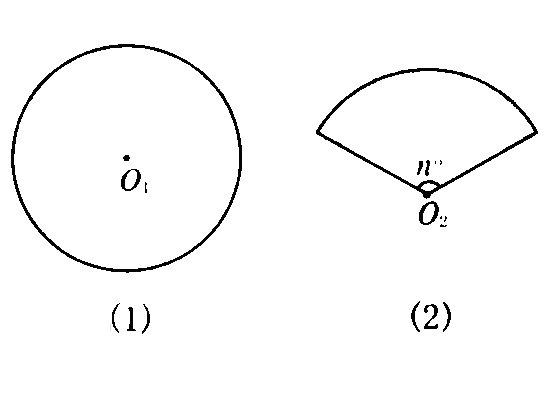
扇形弧長 弧長公式 面積公式 中文百科全書

圆周长计算公式

高中數學必修 一題多解 三角函數 扇形的面積求法 每日頭條

扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典

计算扇形的面积如何计算扇形面积

扇形面积公式大全 搜狗图片搜索

圓面積公式弧度初中數學 幾何 面積與體積公式 Uuogs

扇形面积公式 扇形面积公式画法

弧形和扇形面积 腾讯视频

扇形周長與面積 6年級數學 Grade 6 Math Fan Shaped Area Youtube

Ppt 弧度制powerpoint Presentation Free Download Id

圆的周长与面积 弧长 扇形的面积 玄数

圆的周长与面积 弧长 扇形的面积 玄数

弧长公式扇形面积公式 西瓜视频搜索

数 你好看 任意角三角函数与诱导公式 知乎

2 圓心角所對弦長 弧長與扇形面積 基本觀念 國三上2 2 Live數學學習網 Www Liveism Com 名師葛倫 Youtube

扇形面积的计算公式 扇形面积的计算公式画法

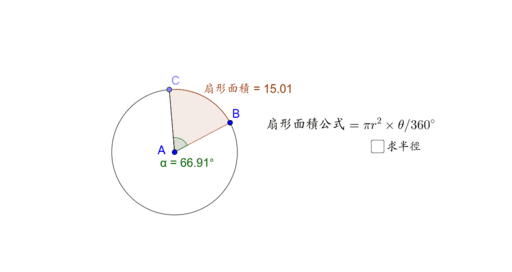
扇形面積公式2 Geogebra

扇形面积的计算公式 扇形面积的计算公式画法

初中數學 圓的性質 扇形面積公式及應用 異常重要 每日頭條

圓的周長與面積 15 如何計算扇形的弧長 Youtube

高中數學必修四 三角函數突破點 二 弧度制及其應用 每日頭條

扇形面积公式和弧长公式 腾讯视频

高中數學必修四 三角函數突破點 二 弧度制及其應用 每日頭條

半圆阴影 圆中阴影部分面积的求法 Weixin 的博客 Csdn博客

圓面積公式的介紹by Cp Ma

扇形面积扇形面积 面积公式 爱华网

Q Tbn And9gctquzgxkvpnpetemepur7grsdbhsaxdn9f8fj5qg3nhqea4si Usqp Cau

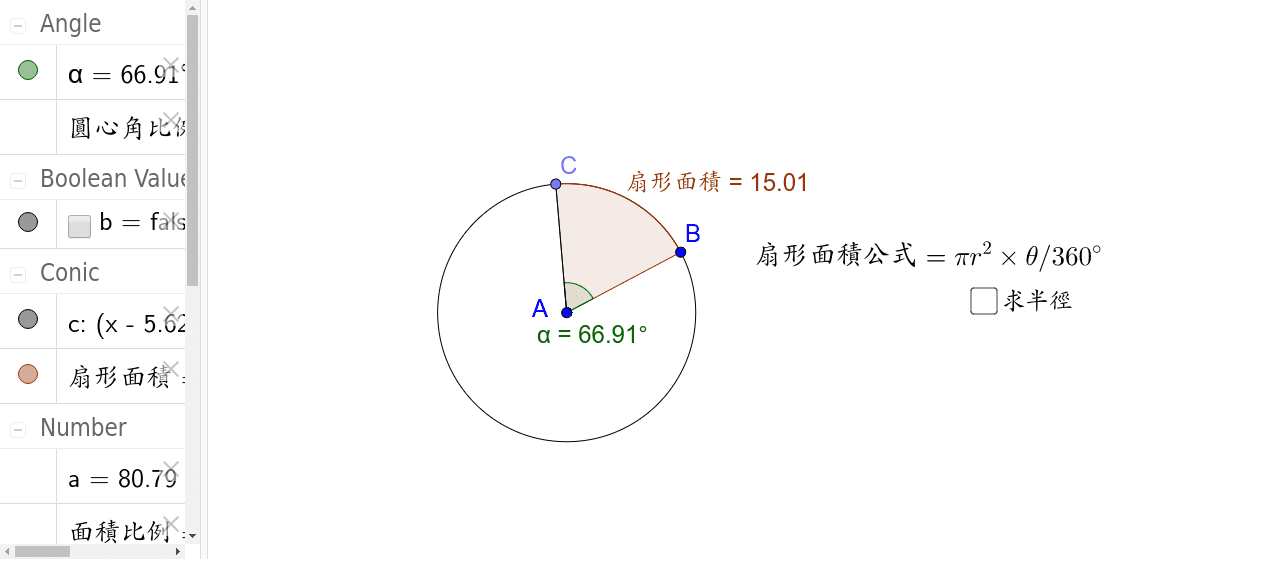
扇形面積公式2 Geogebra

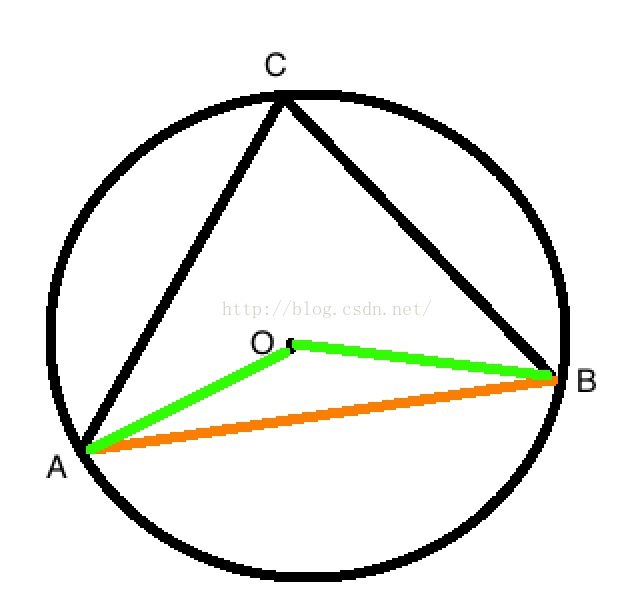
圆周角 圆心角 弦 弦心距 弧长 扇形面积 打鱼还是晒网 Stone 程序员宅基地 程序员宅基地

扇形的面积公式 哔哩哔哩 つロ干杯 Bilibili

弧长公式扇形面积公式 西瓜视频搜索

题型 2弧长与扇形面积公式的计算 哔哩哔哩 つロ干杯 Bilibili

弧长及面积公式 腾讯视频

高校数学 一般角と弧度法 扇形の弧長l R8と面積s 1 2r 8 受験の月

001 弧度 弧長及扇形面積原理 Youtube

弧长公式扇形面积公式 西瓜视频搜索

弧度計算弧長計算公式 弧長公式 N是圓心角度數 R是半徑 L是圓心角弧長 Aypsaf

扇形面积的计算公式 扇形面积的计算公式画法

弧长公式 扇形面积公式 圆 中考网

数 你好看 任意角三角函数与诱导公式 知乎

Incoming Term: 扇形面積 公式 弧度法,